

2022年5月13日,Wiley Interdisciplinary Reviews-Computational Molecular Science杂志在线发表了北京大学化学与分子工程学院刘剑课题组的题为“New Phase Space Formulations and Quantum Dynamics Approaches”的邀稿文章。
在牛顿经典力学框架下,分子系统的所有物理和化学观测量都可以在由粒子位置和动量组成的相空间中描述,动力学由相空间中的经典轨迹刻画。然而,自然界本质上由量子力学支配。当分子系统的量子力学特性显现时,海森堡不确定原理表明粒子的位置和动量并不能够同时被精确确定,经典力学无法胜任。
Eugene Wigner(1963年诺贝尔物理学奖得主)在1932年提出了量子力学的一种等价表示形式—相空间表示理论,建立了量子算符和位置-动量相空间函数的一一映射关系。量子相空间理论有方便的量子-经典对应关系,在量子力学表述和量子系统含时演化等方面得到了大量应用。在量子相空间中容易引入轨迹近似,从而能够胜任大体系的线性标度近似计算,为研究复杂大分子和溶液、固体等凝聚相体系量子性质提供一种有效计算手段。Wigner相空间本质是无限边界相空间,适用于研究连续自由度的量子体系。
由于原子核和电子的质量相差至少在3个量级以上,原子核和电子的运动尺度一般可以分离,即玻恩-奥本海默近似成立。此时,分子体系不涉及电子态的跃迁,称为绝热体系。针对绝热体系,位置-动量相空间理论在原子核量子效应的应用研究已经表现出优势。与之相比,经典分子动力学无法准确描述低温或含氢原子的分子体系;而这些复杂分子体系的原子核量子本征能级十分稠密,波函数表示理论的计算代价巨大。刘剑课题组近年来基于Wigner量子相空间发展出的平衡连续性动力学(ECD)与路径积分刘维尔动力学(PILD)方法能够在保证经典极限、高温极限和谐振子极限严格成立的前提下,保证含时演化过程中量子平衡分布不变,为给定温度的复杂分子系统提供更为可靠的量子动力学模拟手段。相空间量子动力学方法已经应用到水、氨、甲烷、甲醛、过氧化氢和液态水等体系的红外振动光谱和拉曼振动光谱的模拟。结合机器学习拟合技术,计算效率能够进一步提升,有望直接应用到更复杂分子体系的核量子效应模拟。
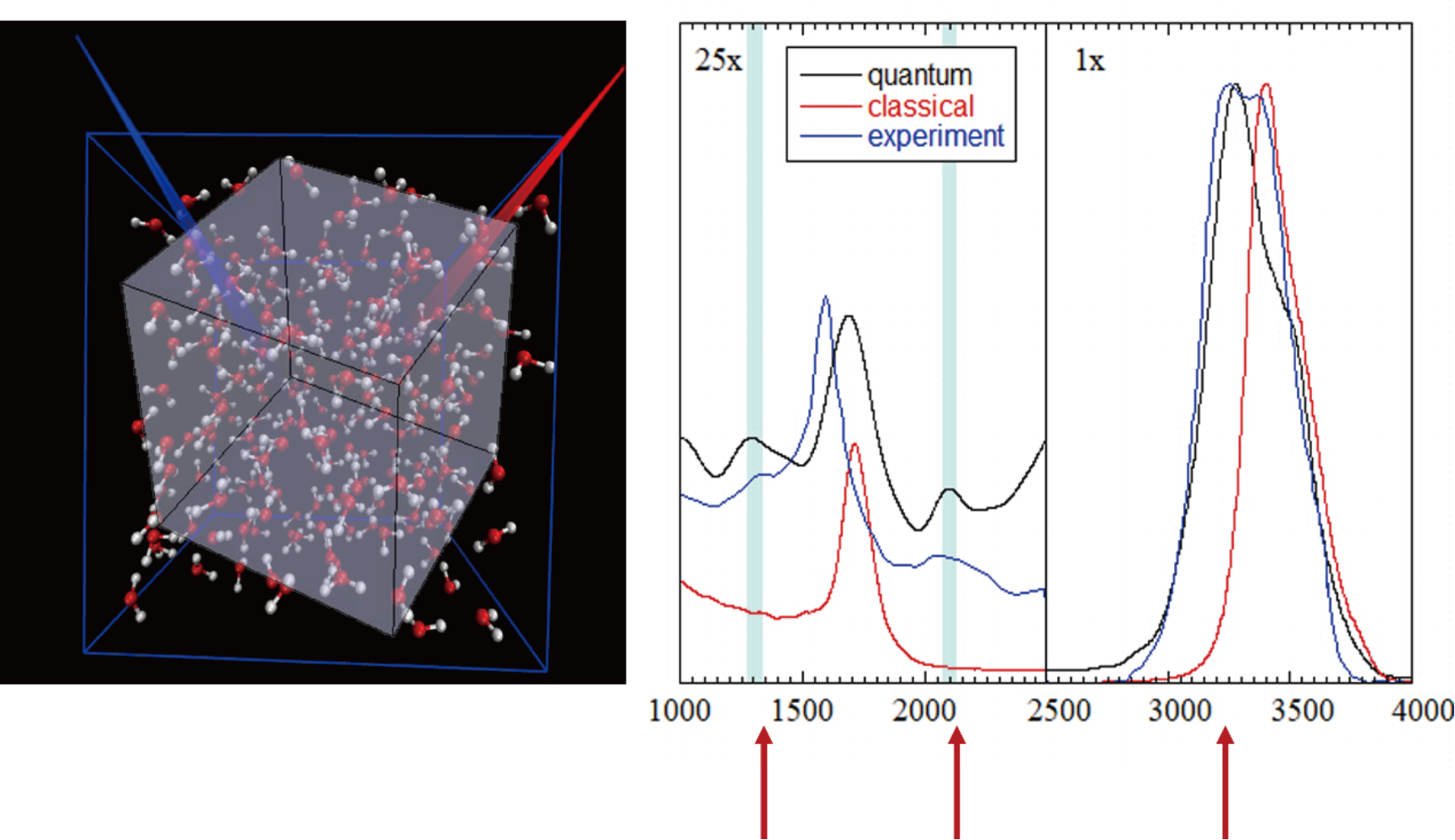
图1:采用Wigner相空间的轨线动力学方法对于液相水拉曼光谱的模拟结果。
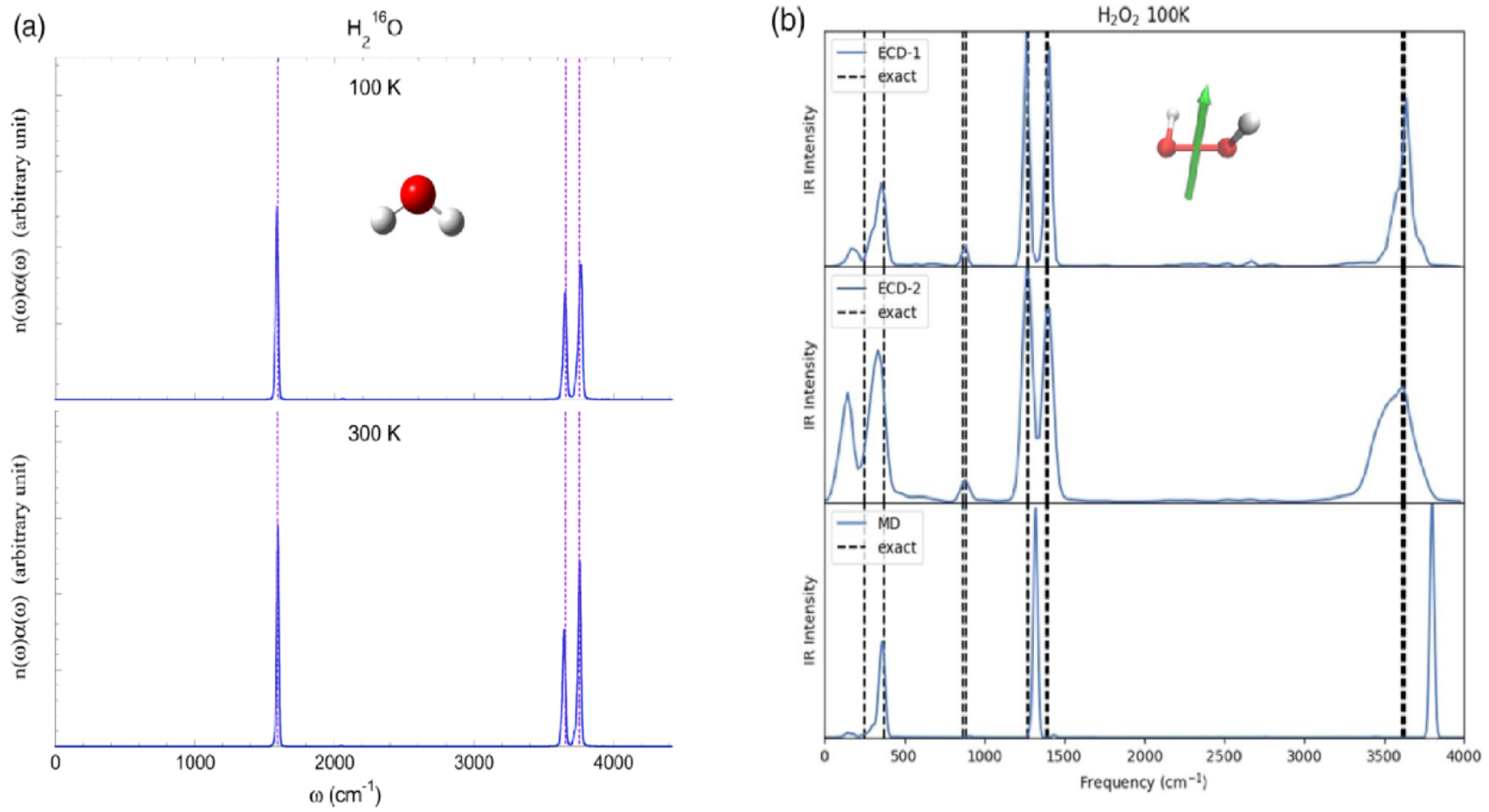
图2:基于Wigner相空间的轨线动力学对于水/过氧化氢分子红外光谱的模拟结果。
当原子核和电子的运动尺度不可分离时,即玻恩-奥本海默近似不成立,分子体系涉及电子态之间的无辐射跃迁,称为非绝热体系。很多光化学和光物理过程(例如,光合作用、光异构化反应、光催化反应、激发态质子转移、电子转移反应、电子能量转移、载流子输运、激子裂分和分离等)牵涉到原子核和电子的耦合运动,必须发展和应用非绝热量子动力学方法才能进行定量研究。由于非绝热体系的哈密顿算符既包含连续自由度(原子核自由度)也包含离散自由度(电子态自由度),传统的位置-动量相空间表示理论亟需进一步发展。
基于2016年的映射哈密顿模型的统一框架,刘剑课题组在2019年首次从电子态布居数之和为1这个必须满足的物理要求出发,将其作为约束条件建立非绝热体系的相空间映射动力学,并后续发展了只含有限数目量子态的离散系统和约束(位置-动量)相空间的一一对应关系。电子态自由度的约束位置-动量相空间和原子核自由度的Wigner相空间相结合可以给出非绝热体系量子性质在广义位置-动量相空间中的严格表达形式。由哈密顿算符在广义位置-动量相空间中的经典映射模型(CMM)可以推导出轨迹运动方程,作为量子相空间刘维尔动力学方程的近似。CMM动力学方法对一系列模型测试体现了其描述非绝热动力学的优点,能够超越目前被广泛使用的面跳跃(surface hopping)和平均场(也称为Ehrenfest动力学)方法。最近的工作里,刘剑课题组将原先基于单一γ因子的映射相空间扩展到使用两个(或多个)γ因子的组合,发展出了新的核与电子统一的映射位置-动量相空间形式,称为加权映射模型(wMM)。图3展示了wMM和CMM对于γ因子的选择比较,以及用于量子纠缠态的可视化表示结果。图4展示了wMM应用于非绝热体系的结果。数值结果表明CMM/wMM在自旋玻色模型(图4a)、原子-光腔相互作用模型(图4b)等体系中,其长时描述都要优于平均场动力学/面跳跃动力学的结果;在Tully的一维散射模型(图4c)中,wMM数值表现良好,尤其是ECR散射问题上,wMM能够准确捕捉到阶型曲线,更超越了原先的CMM/平均场动力学/面跳跃动力学的数值表现。而在吡嗪分子的锥型交叉问题上(图4d),CMM/wMM可以克服Ehrenfest动力学的不足。
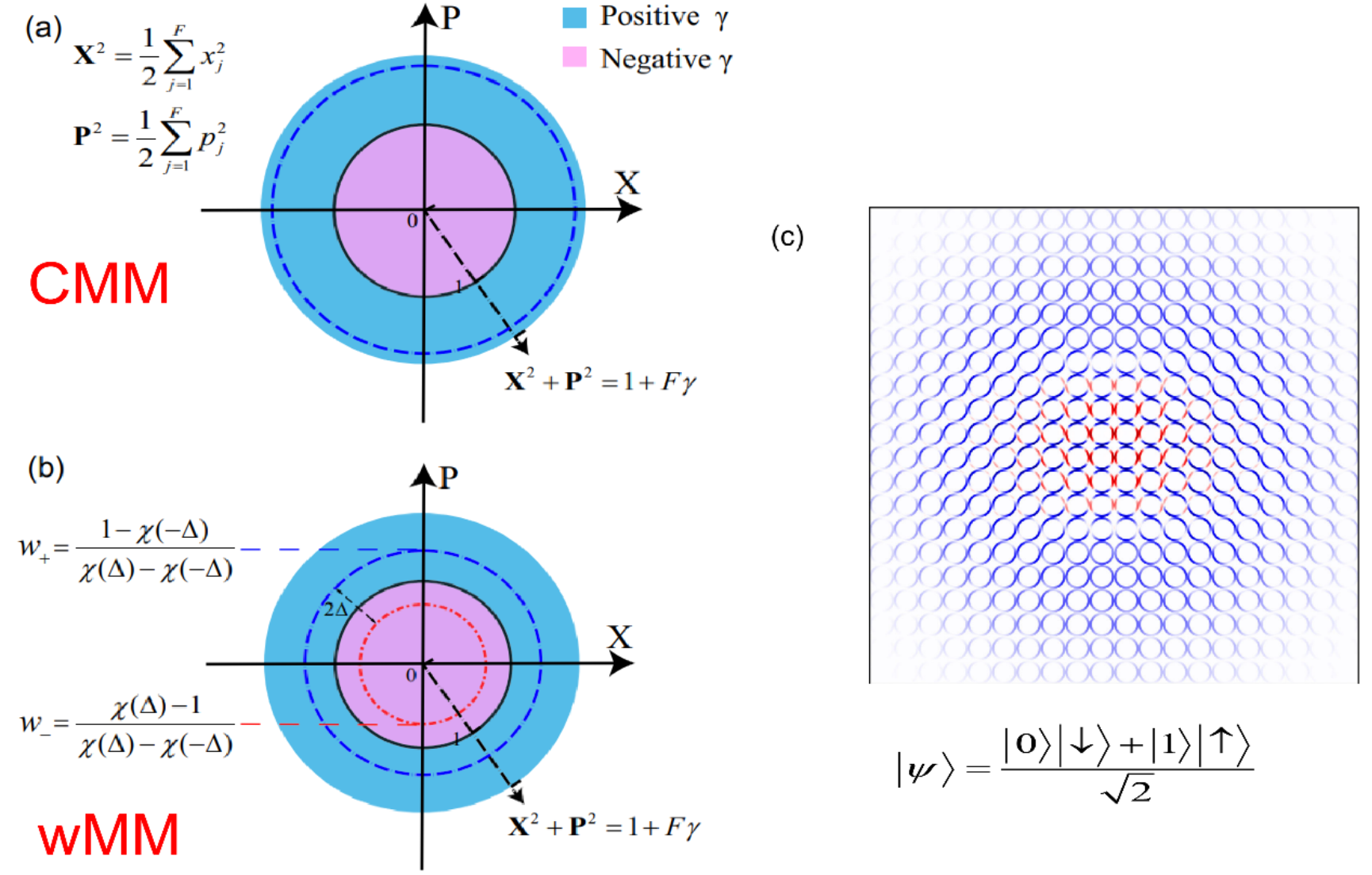
图3:(a)-(b)分别为电子态映射的约束位置-动量相空间CMM和wMM的示意图。(c)是对于核与电子的混合比特的相空间可视化示意图,其中原子核采用了Wigner相空间而电子态采用了wMM相空间。
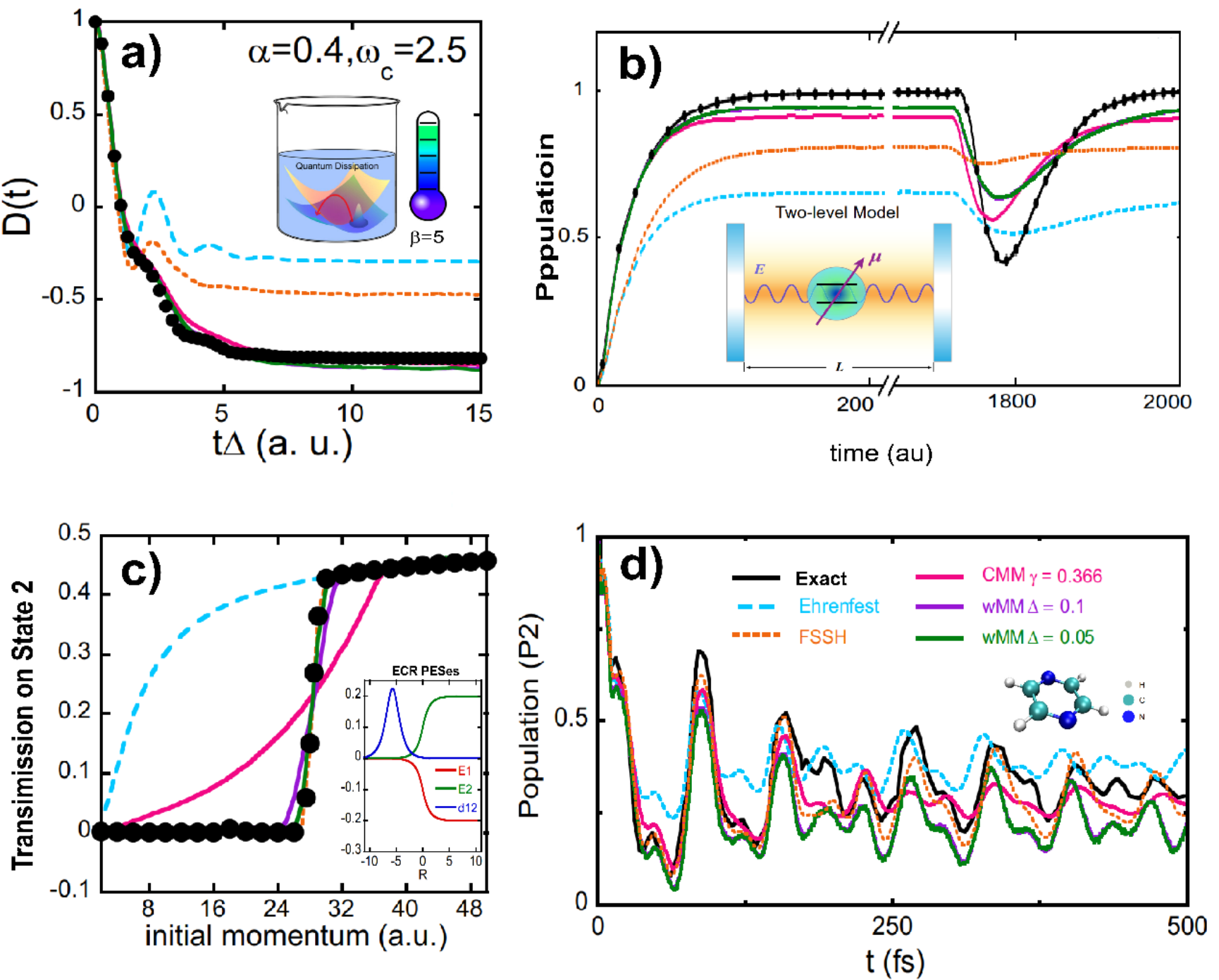
图4:原子核的Wigner相空间和电子态的wMM相空间相结合应用于一系列非绝热问题的计算。
(a)(b)(c)(d)分别展示了自旋玻色模型、原子-光腔自发辐射模型、Tully的ECR模型以及吡嗪锥形交叉模型的计算结果。
此外,该文整理了刘剑课题组前期一系列工作中对于电子态绝热表象和透热表象的相空间运动方程等价关系的推导,关于约束位置-动量相空间和Stratonovich相空间的关系讨论,关于量子刘维尔方程在广义位置-动量相空间的表示形式和近似,等等。
综上,刘剑课题组发展了无限边界的位置-动量相空间表示理论中的轨线量子动力学方法,同时满足对谐振子体系(包含非线性算符的)时间关联函数的准确处理以及平衡系统统计力学物理量不随时间变化这两个最基本物理要求,为动力学物理量的计算提供更可靠手段,并已应用于实际体系振动光谱的研究;提出和发展了包含了有限数目离散态的量子体系的约束位置-动量相空间表示理论,在统一框架下,发展基于轨线的非绝热量子动力学方法(CMM和wMM),并应用到气态和凝聚态非绝热分子体系。该文展示了广义位置-动量相空间表示理论和对应的轨迹近似方法有望于在热化学、光化学的实际凝聚态复杂分子体系的理论研究中提供有效研究手段。
北京大学化学与分子工程学院的三年级研究生贺鑫和吴柏华是这篇文章的共同第一作者,四年级本科生尚游皓和李炳其、一年级研究生程祥松参与贡献,刘剑研究员为通讯作者。该工作得到了国家自然科学基金委、科技部、北京分子科学国家研究中心、化学与分子工程学院的资助。计算资源由北京并行科技、广州超级计算中心以及北京大学高性能计算平台提供。
论文信息:
New Phase Space Formulations and Quantum Dynamics Approaches. Xin He, Baihua Wu, Youhao Shang, Bingqi Li, Xiangsong Cheng, Jian Liu. Wiley Interdisciplinary Reviews Computational Molecular Science, e1619 (2022)
https://doi.org/10.1002/wcms.1619
期刊介绍:
Wiley Interdisciplinary Reviews-Computational Molecular Science于2011年创刊,由Wiley出版社出版,为理论与计算分子科学领域的权威综述期刊,内容涵盖理论与计算分子科学的各个热门方向。2021年影响因子达到25.113。
参考资料:https://www.chem.pku.edu.cn/kyjz/140667.htm
声明:化学加刊发或者转载此文只是出于传递、分享更多信息之目的,并不意味认同其观点或证实其描述。若有来源标注错误或侵犯了您的合法权益,请作者持权属证明与本网联系,我们将及时更正、删除,谢谢。 电话:18676881059,邮箱:gongjian@huaxuejia.cn